ЗНО 2015. СЕРТИФІКАЦІЙНА РОБОТА З МАТЕМАТИКИ (поглиблений рівень)

ЗНО 2015 - Математика. Демонстраційний варіант (базовий рівень)

ЗНО 2015 - Математика. Демонстраційний варіант (поглиблений рівень)

Програма ЗНО 2015 з математики

Критерії оцінювання завдань із розгорнутою відповіддю з математики

Кількість балів, що виставляються за виконання завдань 35 (з геометрії) і 36 (з алгебри і початків аналізу), залежить від повноти розв’язання та правильності відповіді.

Загальні вимоги до виконання завдань з розгорнутою відповіддю: розв’язання має бути математично грамотним і повним.

Методи розв’язання, форми його запису і форми запису відповіді можуть бути різними. Якщо завдання можна розв’язати кількома способами, то достатньо навести розв’язання лише одним способом.

За розв’язання, в якому обґрунтовано отриману правильну відповідь, виставляється максимальна кількість балів.

Під час виконання завдання можна використовувати без доведення і посилань будь-які математичні факти та твердження, що містяться в підручниках і навчальних посібниках, що входять до переліку підручників, рекомендованих (допущених) Міністерством освіти і науки України.

В критеріях оцінювання конкретних завдань містяться загальні вимоги до виставлення балів.

У таблиці 1 наведено оцінювання завдання 35 (з геометрії).

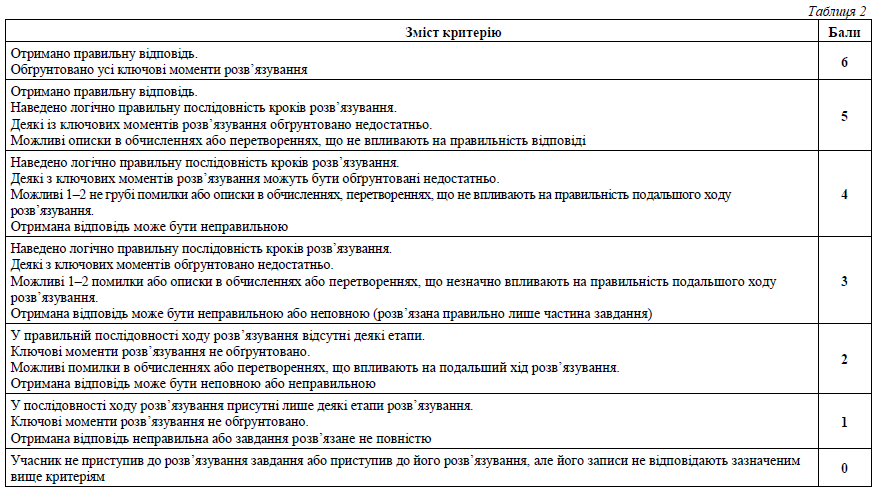
У таблиці 2 наведено оцінювання завдання 36 (з алгебри і початків аналізу).

Увага!

Правильна відповідь за відсутності тексту розв’язання оцінюється в 0 балів.

Розв’язання, що не відповідає умові завдання, оцінюється в 0 балів.

Характеристика сертифікаційної роботи з математики (поглиблений рівень)

Зміст роботи визначається на основі Програми зовнішнього незалежного оцінювання з математики для осіб, які бажають здобувати вищу освіту на основі повної загальної середньої освіти (затверджено Міністерством освіти і науки України, наказ від 01.10.2014 р. № 1121).

Загальна кількість завдань роботи – 36 (30 завдань базового рівня та 6 завдань поглибленого рівня).

На виконання роботи відведено 210 хвилин (130 хвилин на виконання завдань базового 

рівня та 80 хвилин на виконання завдань поглибленого рівня).

Сертифікаційна робота з математики поглибленого рівня складається із завдань чотирьох форм:

Характеристика сертифікаційної роботи з математики (базовий рівень)

Зміст роботи визначається на основі Програми зовнішнього незалежного оцінювання з математики для осіб, які бажають здобувати вищу освіту на основі повної загальної середньої освіти (затверджено Міністерством освіти і науки України, наказ від 01.10.2014 р. № 1121).

Загальна кількість завдань роботи – 30.
На виконання роботи відведено 130 хвилин.

Сертифікаційна робота з математики базового рівня складається із завдань трьох форм:

Методи навчання математики в структурі уроків критичного мислення як шлях до формування компетентності учнів

План лекції

1.1. Структура уроків критичного мислення.
1.2. Методи навчання математики.
1.3. Місце методів навчання математики в структурі уроку критичного мислення
1.4. Формування основних груп компетентностей учнів на уроках математики з використанням технологи «Розвиток критичного мислення» та методів навчання математики.
1.5. Висновок.

Використання історичних відомостей про системи вимірювання величин

З історії розвитку системи одиниць величин

Людина давно визнала необхідність вимірювати різні величини, причому виміряти як можна точніше. Основою точних вимірювань являються зручні, чітко визначені одиниці величин і еталони цих одиниць. В свою чергу, точність еталонів відображає рівень розвитку науки, техніки, говорить про науково-технічний потенціал країни.

В історії розвитку одиниць величин можна виділити кілька періодів.

Геометрія, з давніх часів до сьогодення

Геометрія завжди мала численні практичні застосу­вання. Основними її споживачами були землеміри, реміс­ники, будівельники, художники. Землемірам потрібні були правила вимірювання ділянок землі, будівельники, кори­стуючись геометрією, креслили план споруди, а потім зводили її, користуючись певними, виробленими протя­гом століть правилами, згідно з якими певні геомет­ричні форми частин споруд були пов'язані з умовами їх міцності.

Виникнення геометрії

За переказами, біля входу до Академії Платона було написано “Та не ввійде сюди ніхто з тих, хто не знає геометрії”. З найдавніших часів геометрія вважалася однією з важливих компонент будь-якої освіти взагалі. Насамперед що таке геометрія? Кожний з дитинства звикає до цього слова і твердо вірить, що він чудово розуміє його зміст. Проте, як він не намагався б дати означення гаометрії, завжди знайдеться немало людей, які скажуть: “Ні, це не те”. То що ж таке геометрія? Геометрія настільки вже набула характеру первинно поняття, що легше що-небудь інше означити за допомогою геометрії, ніж геометрію за допомогою чогось іншого. Геометрію легше описати, ніж дати їй означення. Інакше кажучи, доцільно дати уявлення про геометрію аксіоматично, як ми даємо уявлення про точку, пряму, площину.

Піготовка учнів до математичних олімпіад

Черкасова Т.О. 

На відміну від багатьох інших дисциплін математика має предметом свого учення не речі і явища реального світу, а абстраговані від них кількісні стосунки і просторові форми.

З давніх часів математика розглядалася як вища мудрість. Так, старогрецький вчений Платон вважав математику необхідною для більшості людей. Він вказував на "... величезні розвиваючі можливості математики; ... вона будить розум, додає йому гнучкість, жвавість і пам'ятку ..."

В останній час стало проводиться багато різних математичних олімпіад (очних або заочних), математичних конкурсів, які є масовими і популярними як серед учнів, так і серед вчителів. Найбільших успіхів в таких конкурсах добиваються учні з нестандартними здібностями і творчим мисленням.

Для участі в математичних конкурсах, математичних олімпіадах учні повинні мати відповідні знання, бути психологічно і фізично підготовленими, повинні вміти правильно розподіляти час на виконання завдань, долати можливі труднощі.

Творці математики з України

Творці математики з України 

Вебінар. Методичне та дидактичнее забезпечення запровадження Держстандарту під час викладання математики

Презентація. Видатні математики

Книга "400 задач з математичних олімпіад"

Посилання на книгу: Книга "400 задач з математичних олімпіад"

Міжнародний математичний конкурс "Кенгуру"

Кенгуру-2008:

Рівень "Малюк-2" Умови завдань. Розв'язки

Рівень "Малюк-3,4" Умови завдань. Розв'язки
Рівень"Школярик" Умови завдань. Розв'язки
Рівень "Кадет" Умови завдань. Розв'язки
Рівень "Юніор" Умови завдань. Розв'язки

Книги до олімпіад

Зуб Володимир. Міські олімпіади юних математиків / В. Зуб. — К. : Шк. світ, 2008. — 120 с. — (Б-ка «Шк. світу»). Посилання: Зуб Володимир. Міські олімпіади юних математиків
Вороний О. М. Готуємось до олімпіади з математики. Книга 1. (X.: Вид. група «Основа», 2008. — 128 с.) — Книга 2. (X. : Вид. група «Основа», 2008. — 141, [3] с.) (Б-ка журн. «Математика в школах України»; Вип. 5 (65), 6(66)). Посилання: Вороний О. М. Готуємось до олімпіади з математики. Книга 1

Готуємось до олімпіади з математики/ Упорядн. А.Б.Веліховська, О.В.Гримайло. (X.: Вид. група «Основа», 2007.— 160 с. — (Б-ка журн. «Математика в школах України»; Вип. 2 (50)).). Посилання: Готуємось до олімпіади з математики/ Упорядн. А.Б.Веліховська, О.В.Гримайло

Обласні математичні олімпіади. Друге вид., доопр. і доповн. / За загальною редакцією І.М. Конета (Кам.-Под.: Абетка. - 2005. - 344 с.). Посилання: Обласні математичні олімпіади. Друге вид., доопр. і доповн.

І.М.Кривошея, Т.С.Збожинська. Задачі міжнародних математичних чемпіонатів. Посилання: І.М.Кривошея, Т.С.Збожинська. Задачі міжнародних математичних чемпіонатів

Організація та види самостійної роботи на уроках математики та в позаурочний час

План лекції 

1. Вступ. 

2. Принципи побудови дидактичної системи організації самостійної роботи.

3. Самостійне вивчення теорії за підручником. 

4. Самостійне розв’язування задач. 

5. Форми проведення самостійної роботи на уроках математики. 

6. Форми проведення позакласної самостійної роботи. 

7. Дидактичні вимоги до системи самостійних робіт. 

8. Підсумок.

Презентація - 8 клас. Геометрія - Теорема Піфагора

Результати моїх учнів у міжнародному математичному конкурсі «Кенгуру»

Черкаська загальноосвітня школа І-ІІІ ступенів №30 Черкаської міської ради Черкаської області

Міжнародний математичний конкурс «Кенгуру»

(учитель Черкасова Т.О.)

«Кенгуру-2011»: 32 учасника. (133 учня, учасників 104)
Високій результат – 17 учасників (53%)
Добрий результат – 14 учасників (44%)
Учасник конкурсу – 1 учасник (3%)

«Кенгуру-2012»: 28 учасник. (147 учнів, учасників 81)
Високій результат – 4 учасника (14%)
Добрий результат –24 учасника (86%)
Учасник конкурсу – 0 учасників (0%)

«Кенгуру-2013»: 70 учасників. (125 учнів, учасників 133)
Високій результат –4 учасника (6%)
Добрий результат – 47 учасників (67%)
Учасник конкурсу – 19 учасників (27%)

«Кенгуру-2014»: 71 учасників. (123 учня, учасників 169)
Високій результат –15 учасників (21%)
Добрий результат – 35 учасників (49%)
Учасник конкурсу – 21 учасник (30%)

«Кенгуру-2015»: 62 учасника. (114 учнів, учасників 172) (конкурс ще не був проведений)
Високій результат –учасників (%)
Добрий результат – учасників (%)
Учасник конкурсу – учасників (%)

Результати школи у міжнародному математичному конкурсі «Кенгуру»

Черкаська загальноосвітня школа І-ІІІ ступенів №30 Черкаської міської ради Черкаської області

Міжнародний математичний конкурс «Кенгуру»

«Кенгуру-2011»: 104 учасника.
Високій результат – 44 учасника (42%)
Добрий результат – 45 учасників (43%)
Учасник конкурсу – 15 учасників (15%)

«Кенгуру-2012»: 81 учасник.
Високій результат – 4 учасника (5%)
Добрий результат – 50 учасників (62%)
Учасник конкурсу – 27 учасників (33%)

«Кенгуру-2013»: 133 учасника.
Високій результат – 12 учасників (9%)
Добрий результат – 79 учасників (59%)
Учасник конкурсу – 42 учасника (32%)

«Кенгуру-2014»: 169 учасників.
Високій результат – 24 учасника (14%)
Добрий результат – 73 учасника (43%)
Учасник конкурсу – 72 учасника (43%)

«Кенгуру-2015»: 172 учасника. (конкурс ще не був проведений) 
Високій результат –учасників (%)
Добрий результат – учасників (%)
Учасник конкурсу – учасника (%)

Графічні диктанти